titans learning to memorize at test time

general info/abstract

normal bs to explain why quadratic attention doesn’t fit to infinte context so here is the new architecture to solve this

they give a slight explaination of how memory ins understood in transformers here

Recurrent Neural Networks (RNNs) (Williams and Zipser 1989) can be defined as models with a vector-valued memory module M(also called hidden state) with two main steps: Given a new input 𝑥𝑡 at time 𝑡, the model (1) updates the memory using a function 𝑓(M𝑡−1,𝑥𝑡) (with compression); and (2) retrieves the corresponding memory of input using a function 𝑔(M𝑡,𝑥𝑡)(see §2.1 for details). Similarly, Transformers can be seen as architectures with a growing memory and two similar steps. That is, the pair of key and value matrices acts as the model’s memory, and the model: (1) updates the memory by appending the key and value to the memory (without compression), and (2) retrieves query vectors’ corresponding memory by finding the similarity of query and key vectors, which is then used to weight the value vectors for the output.

then they go on to explain in short how we have linear transformers and rnn to be scaled to use in memory which is like how they map the key value to a fixed attention matrix to be later retrieved instead of having it all incontext. (kv cache rag) leading to some questions i think they answer in this paper.

Therefore, this perspective motivates us to ask: (Q1) What constitute a good structure for the memory? (Q2) What is a proper memory update mechanism? (Q3) What is a good memory retrieval process? (Q4) How to design an efficient architecture that incorporates different interconnected memory modules ? (Q5) Is a deep memory module needed to effectively store/remember long past?

roadmap

to answer the above questions they design a neural memory module with this roadmap

if an event that surprises the model (violates expectations) is more memorable this is done by measuring the gradient of the neural network with respect to input in associative memory loss. i think what is meant here is that if a new input is out of distribution to the expected inputs it should give a bigger gradient when checked agains the the current context. this makes sense since you need to remember stuff you don’t know about more than the stuff you already do
there is also a decaying mechanism to handle limited memory and as they say its a generalization of forgetting mech in rnns (lstms)

then they talk about titans so it has three modules a) core: short term memory (attention and context prolly) b) long term memory: this has the neural long term memory that they are using the above stuff for c) persistent memory: sort of like facts ig they arte a set of learnable parameters ig it would probably be just a bunch of weight matrices that can be trained to store facts on given input (this is important can be used for DNC )

they also do varients of titans incorporating memory as (i) a context, (ii) a layer, and (iii) a gated branch.

long term memory

we get the simpler idea from this paragraph main things we need to know is so essentially there are two loops

that is in the pretraining that just teaches the model how to store information
that based on the learning and the gradients stores information

in the second loop: this part actually only updates the model state $M_{t}$ based on the prev response it’s a meta model online learning and surprise metric to store the info from past information which is then further broken down to also incorporate prev surprise since multiple surprising events can lead to a smoother gradient curve the information is still surprising but since all the past info was also surprising the curve becomes flat so the final equation is : $M_{t} = M_{t - 1} + S_{t}$ where $S_{t}$ : $S_{t} = (𝜂 t) S_{t - 1} - 𝜃 t \nabla ℓ (M_{t - 1}; x t)$ 𝜂𝑡 (is time dependent decay) and theta acts as a momentum where $S_{t - 1}$ is the surprise factor from the last token and the delta l to mt-1 for xt token is the gradient between the expected key value and the key value

how do we calculate surprise ?

this part was a little confusing to me as in what exactly is the gradient of what are we comparing to know the surprise factor. so given a token n before predicting the next token n+1 we get the relevent info with the meta model at M(n) and corss check with n+1 llm to find if its new information and then gradient to find surprise factor. this is handled like an online learning problem the weights are updated as it infers the context so more or less dynamic memory. so the gradient acts as a signal not but not to calculate the loss

for the actual model the memory is stored as key value pairs like in transformers you have a given $x_{t}$ we have two linear layers converting x_t to k , v so the model learns the association between these k , v at test time and for each k ( $x_{t}$ ) that appears finds the appropriate V pair

let’s understand the equation for why we have all those terms

in the first loop the model is the pretraining one the loss for the model is standard mean squared loss, it is pretty easy actually based on the given model states and output it gives output for each next token and calculates the loss between the k and v to find the associations the loss formula is $l (M_{t - 1} : x_{t}) = ∣∣ M_{t - 1} (k_{t} - v_{t} ∣ ∣_{2}^{2})$ and now they have changed the prev formula to add a forgetting mech :sob: where $α_{t} \in [0, 1]$ describes how much information should be forgotten (they also point out later in the paper how this is cloesely similar to gating mech in RNNs)

this learning module is a simple MLP with >=1 layers they did it for the sake of simplicity but that fancier architectures can be used as they mention some other ones but i don’t really care for it right now maybe when i hit a roadblock i will see to it although through experimentation they know deep memory modules are more effective

retrievel

is quite simple actually u just pass the quetry token that we get when we get $q_{t} = x_{t} W_{q}$ The output $y_{t} = M^{*} (q_{t} )$ represents the retrieved information, where $M^{*}$ denotes the LMM’s forward pass without weight adjustments. the $W_{q}$ is a linear layer to convert (or project) the input

then 3.2 section is about parallelizing the training of long term memory but i don’t care for right now maybe when actually writing the code i will later read and add the section

then we move onto persistent memory which is actually part of the “memory as a context” architecture so let’s first see persistent memory and we will see how lmm and persistent memory fix in it

persistent memory

$x_{n e w} = [p 1 p 2... p_{N_{p}}] ∣∣ x,$ then they go on to explain how LMM(long term memory) is a contextual memory so as to it only depends on whatever context is passed throughout the process then they talk about something interesting on how FFNs after attention are data-independent weights if we use softmax between them

In the Transformer architectures, there are fully connected layers after the attention module, which are shown to be similar to attention weights but with data-independent parameters. That is, Sukhbaatar, Grave, et al. (2019) showed that replacing the ReLU in fully connected layers with Softmax can results in an attention-like weights, in which weights are data-independent:

this is very interesting maybe i should read this paper later (it has only 5 pages wow) it comes down to this you can remove the relu activation from the two linear layers in FFN and replace with softmax and have $FFN (x) = W_{V} S o f t ma x (W_{K} (x))$ so for some reason these are just a bunch of learnable vectors always appended to the context for some reason oh wait not for some reason they give three reasons this seems so stupid to me what the fuck??? the best explaination is that the attention with casual mask as bias towards initial tokens 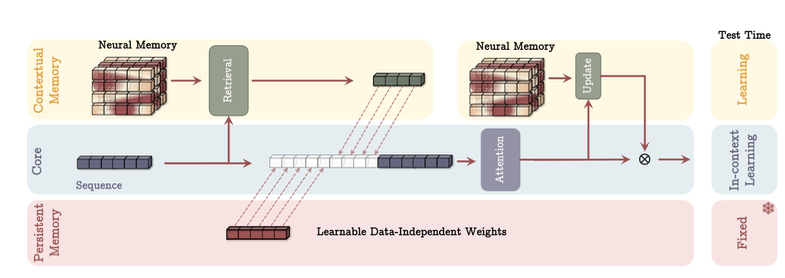this is how the “MAC (memory as a context)” architecture looks like idk about this persistent memory this seems like an overdo will keep this on hold for now the results seem good enough ig atleast for LMM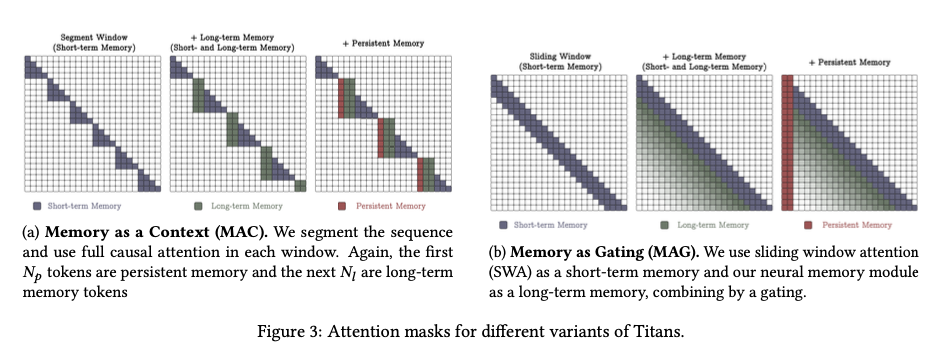

memory as a context

in MAC this was pretty weird the first have the original sequence $S_{t}$ where the convert it into b chunks of size c and then pass it and use the segments to query for the new token $h_{t}$ like this: $h_{t} = M_{t - 1}^{*} (q_{t})$ where $q_{t} = S (t) W_{Q}$ , and then we concatenate these and get $S_{t}$ $S^{'} (t) = [p_{1}, p_{2} \dots . p_{Np}] ∣∣ h_{t} ∣∣ S_{t}$ which we then pass through the attention part or the middle layers of an LLM

Note: not the whole llm just the middle so ig it has to be the correct size i am not sure then never mention what the fuck Attn is , but they also don’t mention where they get the LLM from in this whole flow so i am assuming this is from the transformers model itself

so we get $y_{t} = A tt n (S^{'} (t))$ which we use to update our $M_{t - 1}$ state to $M_{t}$ and we query it again with $y_{t}$ $o_{t} = y_{t} \otimes M^{*} (y_{t})$ which again they never tell if o_t is the final vector or whatever is happening so i assume after the attention module ends and the last linear layers are left it uses this $o_{t}$ vec and the linear layer and softmax over it.